"Degenerated" Cases of Tensity Function and the Degree of Genre Characteristics Expression in i Musical Piece (Experiments of Quantitative Analysis Applied to Pianoforte Miniatures of 18th-20th centuries)
In musical science the key notion linking historically established types and species of musical products with means and terms of their performance and perception is genre. In the framework of such an approach genre of music becomes the principal component of music's «genetic code» and succession carrier in the process of historic development. Genre's fundamentals, first and foremost -motion, declamation and singing - are expressed in this or that way in any theme of any piece of music. As a rule, the impact of genre's fundamentals on form and content parameters of music is assessed intuitively. At the same time today there exists a mathematical toolset to adequately describe cases with various types and degrees of uncertainty - that is, the theory of Fuzzy sets (Zadeh, 1965). In relation hereto it is interesting to consider the issue of quantitative presentation of the genre characteristics expression in music.
In this research the impact of motion is considered, concerning the characteristics of tensity function in musical pieces of XVIII-XX centuries. Sixty-one randomly selected pianoforte miniatures, belonging to the so-called «program» music, were processed. The tensity function in each piece was determined as Fuzzy set FN = (FP, HP, RP), where FP, HP and RP are Fuzzy sets describing the number of texture, harmony and rhythm «events» per time unit (their density):

where the <Average density> is a function of interval contents, intensity and register.
The density of rhythmic events was determined using the quantity of attacked sounds, the density of harmonic events - based on the number of accord changes, and the density of texture events — as an average degree of accords' consonance/dissonance (see also Zubareva, 2002; Kulichkin, 2002).

|
| Figure 1a. J.S. Bach. Preludio I. Rhythmical pattern |

|
| Figure 1a. J.S. Bach. Preludio I. Harmonic Density |
|
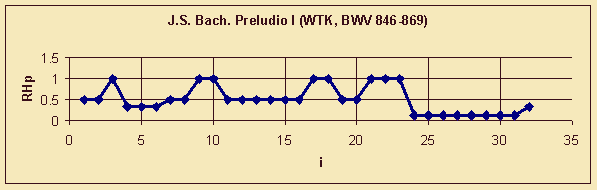
| Figure 2. J.S. Bach. Preludio I. Diagram of density of rhythm and harmony events. |
|
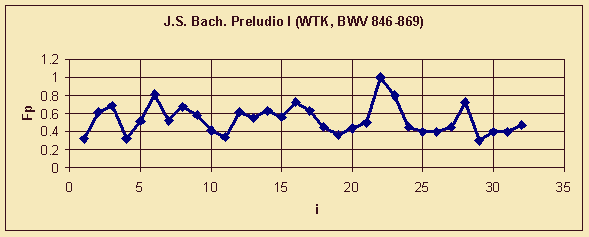
| Figure 3. J.S. Bach. Preludio I. Diagram of density of texture events. |
Let us demonstrate this approach to the interpretation of results on the example of Preludio I from Volume 1 of J.S. Bach's «Well-Tempered Clavier» (Fig. 1-3). In 32 beats out of 35 two of three parameters (HP and RP) are constant values (Fig. 1). At the same time, there is a development of an independent rhythm and harmony process, which is expressed through interchange of sound events in the bass voice (Fig. 3).
The comparison of curves' profiles in Fig. 2 and Fig. 3 reveals their central symmetry over i=14. There are four maximums of the rhythm and harmony curve, the utmost being synchronic with the maximums of the texture curve, and the intermediate one being complementary to the texture ones. The discovered symmetry may be attributed to the statics of «continuing state», modelled by the composer in this piece. At the same time, the dynamic forces are also active in the Preludio; they reveal themselves in the culmination value of the texture density in the beat 23, as well as in the higher event saturation of the rhythm and harmony process after the central symmetry point, providing for the preparation of the following Fugue.
Having analyzed the 61 diagrams of the pianoforte piece, we came to the following conclusions:
1) In the miniatures where motion component dominates, one of three tensity parameters is «degenerated», i.e. constant throughout the whole piece or its section, or - which is actually the same in mathematical terms - strictly periodic. Texture density less often turns out to be such parameter, which may be attributed to the artistic target of expressing motion. In this case the role of texture density becomes decisive in setting the climax;
2) «Degeneration» of one parameter is especially pronounced in «utile» samples of music, receding alongside with «erosion» of links between themes and genre protoplast;
3) The impact of tensity function (and its elements) on the degree of genre characteristics expression may be defined as dispersion of «degenerated» parameter: the less the dispersion, the higher the degree of impact.
4) The rare case of degeneration of two of the three density parameters evidences the lack of coincidence between the motion processes of the foreground and the background temporal statics. This correlates well with the theoretic notion of the presence of several levels in musical forming.
The results obtained allow us to attribute the analyzed parameters to a general phenomenon studied by various sciences. Thus, physiological data evidences high density of internal apprehension, while linguistics proves the important role of informational density in the conceptual execution of new knowledge. It is quite possible that the examined changes in density of sound events and their consequence, i.e. changes in tensity, belong to the universal means of coding any information (biological, scientific, aesthetic, etc.).
References
Kulichkin, P.A. (2002). About researching one's own work. In: Bulletin of Psychology and the Arts. Vol. 3, №2, 53-54.
Zadeh, L.A. (1965). Fuzzy sets. In: Information and Control Systems. Vol. 8, 338-353.
Zubareva, N.B. (2002). Tochnye metody v issledovaniyi protsessov musykal'nogo formoobrazovaniya. In: V.V. Malanin (Ed.), Istoriya I metodologiya nauki (pp.94-103). Perm: Perm State University. [Quantitative methods in research of musical form].