"Musical Arithmology": in Search for Quality in Quantity
Abstract
One of the branches of numerical approaches in modern musicology is connected with studying "objective" properties of a harmonic vertical - "textural density" (which originates in researches by Paul Hindemith and later on evolves in the works by Yuzef Kon). As textural density we can register the changes of inter-disposition of tones within a sound construction and the updates of tonal composition of the harmonic vertical. Thus, these three parameters (textural density, rhythmical pattern and harmonic pulsation) gain the status of musical events. The whole dynamics of event density in musical composition may be described in mathematical terms using fuzzy sets. The analysis of the event pattern allows for drawing some conclusions about the role of density and its changes in the processes of formation, and demonstrating it using the examples of corresponding graphs in "Menuet" by W.A. Mozart and the first part of the piano sonata No. 19 by L. Beethoven. The research of 181 piano pieces allows us to say that the dynamics of events density changes are the means of realizing the universal principles of structural thinking.
In 1922 Russian thinker Pavel Florensky wrote: "Modern scientific thought is discovering a necessity in a well-elaborate mechanism of numerical functions and numerical studies in general - what is called arithmology. One can anticipate, [that] underdevelopment of arithmological disciplines will become a stumbling block for the new natural philosophy and will require in the nearest future a focus of mathematical efforts on this very aspect" (Florensky, 1971, p.506). Despite the fact, that the term "arithmology" has not been generally acknowledged, the quote may be called a prophesy, as numerical approaches were gaining in importance in the ХХ century in various fields of science. One of them was the field designated by Florensky as the "new natural philosophy", or, to be more precise, a whole range of fields, which imply philosophical reflection, and where philosophical explications of cultural universals can emerge in primary form. Those fields, undoubtedly, include modern musicology with its characteristic intention to transform unconscious fundamentals of artistic thought into generalized categorial forms, actively "working" for the process of musical realities' cognition.
Such studies unfolded in different directions, one of which originates in theoretical researches of German composer Paul Hindemith in the sphere of interconnections between "objective" properties of a harmonic vertical and its "subjectively" perceived qualities. At present several approaches to interpretation of such qualities and opportunities of their quantitative analysis are known. Thus, Paul Hindemith, who denominated this quality as a "harmonic tension", considered that it depends on interval composition of chords, and built a peculiar system of their classification upon this concept (Hindemith, 1940, S. 125-129). The examined property of the vertical plays a very important role in music. Here is an example, where Hindemith shows variation of harmonic tension, where tonal relations play no role, and below is a figure, which visualizes such


Figure 1. Variation of "harmonic tension" (Paul Hindemith's example).
This figure reproduces the degree of harmonic tension very approximately, but it shall not be evaluated in terms of precision. The key point here is that it demonstrates the desirability of graphical representation of a harmonic pattern: "Numerical (and possibly, graphical) representation <...> of results would give a demonstrative picture of harmonic dynamics in time" (Kon, 1971, p. 305).
Later on, using Hindemith's gradation of intervals and taking into account compound as well as simple ones, Russian musicologist Yuzef Kon derived the formula of chord density (Kon, 1971, p.309):
where D is the general density of a chord,
I is the index of an interval's density:
|
Interval |
I |
|
Tonic |
0 |
|
Octave |
1 |
|
Fifth |
3 |
|
Forth |
4 |
|
Little sixth |
5 |
|
Large third |
6 |
|
Large sixth |
7 |
|
Little third |
8 |
|
Little seventh |
9 |
|
Large second |
10 |
|
Large seventh |
11 |
|
Little second |
12 |
|
Triton |
13 |
Table 1. Values of index of density I for various intervals.
that the compound interval can include;
R is the register index [Because of down level of computing technology, that Yuzef Kon could use in 1971, he approximated this index by natural numbers, but now it's better to associate R with a continuous function, for example - with logarithm of bass pitch].
Kon's formula allows calculating the density of any chords irrespective of the structure of musical texture, in which they are included, that is why the issues arising from the differences of exact textural realizations of a chord, has a methodological, and not a technical character. Let us now examine these issues and the variants of their solutions on the example of Chopin's Nocturne op. 9 No. 2. In this and similar cases density can be calculated for a chord, conventionally reduced to a vertically compact form of representation:

Figure 2. F. Chopin. Nocturne op. 9 No. 2.
[Here it not the question of getting exact results, but of demonstrating different approaches to measurement of textural density, that is why the relations between melody and accompaniement, which complicate the procedure of calculation, are not taken into account]

Figure 3. F. Chopin. Nocturne op. 9 No. 2. Textural density calculating (the simplest method)
Another approach suggests defining density of each element of a textural figure:

Figure 4. F. Chopin. Nocturne op. 9 No. 2. Defining density of each element of a textural figure.
Do the reduced values of textural density reflect the measured characteristics of musical events? Probably not, whereas only the textural figure on the whole, and not its components, possesses qualitative definition, which means that in order to define its density it is necessary to modify Yuzef Kon's formula in the following manner:
[The row (1, 2, ... n) designates the number of elements in a textural figure]
The results of calculations under this formula give considerably lower values of textural density (see Figure 5), than those received for a compactly disposed chord. This is quite natural, whereas the introduction of pitch complex tones contributes to reduction of excess massiveness at aural perception of a musical piece.

Figure 5. F. Chopin. Nocturne op. 9 No. 2. Textural density calculating (the exact method)
It is evident that the pattern, formed by the density changes of compact, or conventionally regarded as compact, chords, occupies an intermediate position between harmonic and textural patterns. This way of measuring the properties of musical and textural vertical is optimum for chord texture; it is also convenient in those cases, when any other type of texture persists from the beginning to the end of a musical piece, whereas here the difference of real density of phonation from the density, defined for a compactly disposed reference, may be neglected. The insufficiency of this method is revealed, when a musical piece features the changes of musical texture. In order to reflect such changes, we suggest applying Kon's formula in a modified form: while the calculations according to the original formula give an idea about the "harmonic weight" of the chord (this term is to be met with already in Hindemith's works), the calculations made under the modified formula allow establishing a relation between "harmonic weight" and "textural volume", which is defined by the notion "density".
Having performed the described calculations for a certain musical piece, we can reflect the obtained results in graphical form, which gives a visual idea about phonic properties of musical texture and their changes. At the same time we register the changes of inter disposition of tones within a sound construction and updates of tonal composition of the harmonic vertical, which gain the status of musical events. This conclusion corresponds to the definition of Russian musicologist Yekaterina Ruchyevskaya, who suggests considering "an event, moving the form, primarily <...> the change of structural elements functions, which is mainly related to the change of introduction of a new element" (Ruchyevskaya, 1998, p. 50). Further on, Yekaterina Ruchyevskaya builds a hierarchy of musical events, including into the events of phonic level not only the changes of "density and quantity of sound", examined by us, but also the changes of a pitch position, modal significance of tones, time values, accents, sound colour (timber), articulation, etc. (Ruchyevskaya, 1998, p. 51). Some of those events (including modal significance of tones, timber, articulation) actively resist the attempts of their measuring, whereas for other quantitative approach turns out quite natural. The latter comprise rhythmical pattern and harmonic pulsation.
Regarding rhythmical pattern an original way of numerical representation was discovered and approbated by Yuzef Kon, who suggested designating the stressed moment by 1, and unstressed moment - by 0. "The advantage of such method of depiction, - the researcher wrote, - is that we obtain here certain numerical designations, consisting of only 0 and 1. <...> these figures may be regarded as numbers presented in the binary system. <...> The value of each number represents a relative "rhythmical weight" of each bar. Such method of depiction is (if we indicate the sequential number of the bar) isomorphic to its object - rhythm" (Kon, 1971a, p. 226-227). [Today this method can not be acknowledged universal. The principal reason here is the orientation on a binary system inconvenient for graphical representation, which is imposed by the capabilities of computing technology contemporary to Yuzef Kon. The depiction of rhythmical pattern as a total of stressed elements is more rational, however, at the same time opposition of stressed and unstressed elements loses sense, and the resulting total shall be better called the sum of attacked sounds.] Harmonic pulsation may be interpreted in a similar was with the change of pitch construction regarded as a "stressed moment", and preservation of a previous construction - as an "unstressed moment".
The described procedures allow receiving of quantitative data on certain type of events and their distribution in time of a musical piece, but do not provide for comparison of received event characteristics due to principal difference between the examined phenomena themselves and means of their quantitative evaluation. In order to make the results of the performed calculations comparable, it is necessary to relate them to artistic effects, arising from varying of the event flow. The principal of them if the impression of tension received by the listener (or created by the composer), the level of which allows him to orient himself in the processes of image development and compositional unfolding of a musical piece.
Thus, in mathematical terms, the dynamics of event density (as well as changing "the impression of tension") in musical composition may be regarded as a "class of bars" with a continuum of grades of membership (depending on the level of tension). Such classes are known as fuzzy sets. [A fuzzy set A in X is characterized by a membership function fA(x) which associates with each object x in X a real number in the interval [0, 1], with the value of fA(x) at x representing the "grade of membership" of x in A.] (Zadeh, 1965, p.339). We have introduced the following fuzzy sets uniting the values of a certain parameter, having impact on event density:


where:
i - is the number of a bar,
n - is the total number of bars,
fR(i), fH(i) and fT(i) - are membership functions:
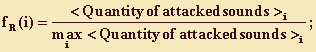
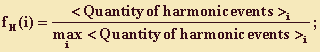
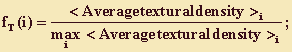
where each <Averagetexturaldensity>i is calculated like D in (1) and (2).
Using the above method, we have calculated the event density in 181st fortepiano piece and have built graphs on their basis, reflecting the eventive pattern of those pieces. On the graphs the multitudes of points, formed by bar-by-bar values of membership functions, appear as geometrical figures - lines (primarily, curves) and surfaces (primarily, triangles and trapezoids). Interpretation of the received graphs is aimed at correlation of changes dynamics of event density with the processes of musical image unfolding and development, that is why analytical operations with figures as opposed to separate points, are more reasonable. In the course of such analysis the application of geometrical terms ("line", "curve", "trapezoid", etc.) appears quite correct, which allows their use without quotes.
The analysis of event pattern makes it possible to draw a conclusion about the role of density and its changes in the processes of formation. Let us demonstrate this on the example of sound events density graphs in "Menuet" by W.A. Mozart. Figure 6 distinctly demonstrates that the ends of sections of a simple three-part form are marked with declines of density of rhythmical and harmonic events in 16th, 28th, and 44th bars. The border between the sections is also emphasized by a transition to a new mode of change of sound events density, which is visually registered as a change of event pattern profile (flow). Thus, a contrasting change of graphical contour from the 17th bar serves as an indicator of the middle part beginning, and the return of the initial configuration from the 29th bar - an indicator of the recapitulation beginning. The changes of events density express themselves similarly to purely musical means of constructions delineation: the dividing role of minimum density of sound events is comparable to the role of cadences, pauses, motion cessations; analogy of changes modes of events density - to manifestation of thematic repeatability, and transition to a new mode - to change of thematic material. In Mozart's "Menuet" specific and non-specific caesura-creating factors act simultaneously, therefore the structure of the musical piece is brought to the listener with utmost clarity and distinction.
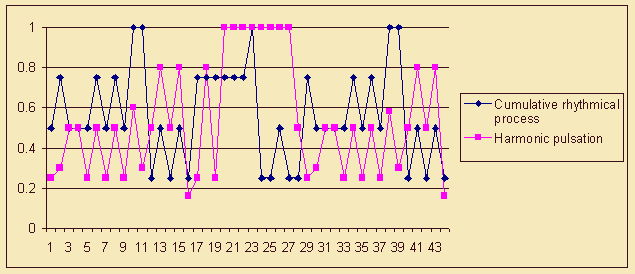
Figure 6. W.A. Mozart. Menuet. Membership functions fR(i) (Cumulative rhythmical process, according to the fuzzy set R) and fH(i) (Harmonic pulsation, according to the fuzzy set H).
Another aspect of formation capabilities of events dynamics is related to the growth of membership functions values, which is one of the means of preparing and execution of climax. In the examined case all the "peaks" of harmonic events (in the 10th, 23rd, 38th bars) are matched with local peaks of musical material development [It should be noted that local culminations of utmost parts are located in the points of golden section (in 10th and 38th bars, which is the 10th bar of the reprise), and the culmination of the middle part - in the center of "Menuet" (on the border of the 22nd and the 23rd bars)], moreover, in the utmost sections the acceleration of harmonic pulsation is accompanied by the growth of rhythmical pattern saturation, and in the middle section the maximum value of harmonic events density falls on the center of the zone of maximum density of harmonic events. Based on interaction of several event flows we can range the maximums of membership functions, regarded as culminators. With the same value of harmonic pulsation density, equal to 1, the central maximum turns out the strongest culminator as compared to the utmost ones - due to accompanying growth of the number of rhythmical events the peak of the 23rd bar becomes the general culmination of the piece.
Apart from "dot" and "zonal" impact on the form of a musical piece, the density of events is directly related to execution of compositional function, typical of this or that fragment of the piece. Thus, the realization of the development function by the central section of "Menuet" is ensured primarily by the growth of events density of the rhythmical flow, the value of which amounts to 0,82 on average as compared to the average value of 0,43 in the utmost sections. At the same time harmonic pulsation retains the same frequency (0,6), close to expositional (0,56), and such ratio of compositional "burden" on harmony and rhythm is typical of the developing sections of Mozart's contrary to the generally acknowledged opinion on principal importance of chord changes rhythm acceleration.
The textural parameters of the examined piece are of special interest. In most cases the calculation of musical texture density may be performed according to Kon's original formula; the exceptions are only the five 5 (from 24th to 28th) bars of in the end of the middle part, where melodic and harmonic figuration duplicated in an octave clearly outlines the contours of the chords, which take part in the reprise preparation. Those chords may be conventionally represented compactly and to define numeric indicators for this form of harmonic vertical according to the same formula. In this case we get the figure of textural weight. On the other hand, such figuration may be regarded as a linear construction, possessing a density value different from the zero only due to octave duplication. The results received in this case would be the values of textural density. Both approaches are almost equally grounded, and the results of their application, presented at Figure 4, reveal different sides of participation of musical texture vertical in formation.
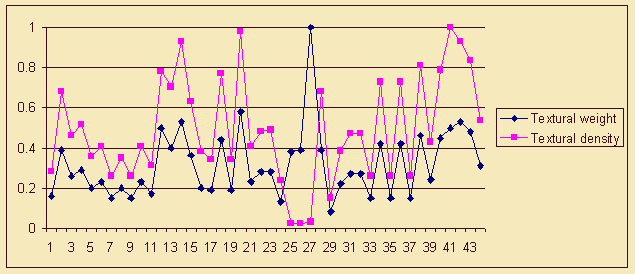
Figure 7. W.A. Mozart. Menuet. Two versions of membership function fT(i) that is according to the fuzzy set T (Textural weight and Textural density).
The maximum value of textural weight falls on the 27th bar; this peak together with the preceding rise depicts a violent growth of tension, extremely important for creating a compositional inclination to reprise. A principally different role is played by the maximums of textural density. The first of them is located two bars before the end of the first section of "Menuet", and the last - three bars before the end of the whole piece. It is logical to suppose that the growth of textural density contributes to absorption of energy accumulated in climaxing zones, thus becoming one of the means to execute compositional function of completion. The specificity of formation capabilities of the examined properties of musical texture is expressed most vividly in the middle part of the piece, where the central peak of textural density coincides with the beginning of the zone of events density of the rhythmical flow, and the peak of textural weight - with its completion. At the same time the release from excess density promotes the quickest motion to culmination, and the further accumulation of weight - the post-climax slowdown.
Due to the performed analysis we have got the opportunity not only to reveal the principal forms of interaction of musical events density with specific formation means, but also to discover the traces of a special - purely eventive - organization of the piece. Thus, on Figure 8 we can see clearly the initial fragment (from the 1st to the 5th bar), including the harmonic peak of the second bar, the rhythmical peak of the 2nd-4th bars and the double textural peak of the 2nd-4th bars, summing up the properties of two other rows. The second fragment (from the 5th to the 11th bar) features a large-scale extension and formation of a synchronic for all the curves triple peak, the third top of which, marked by high frequency of harmonic pulsation, becomes a local culmination. From the 12th bar the initial figure of a double peak comes back, which is accompanied by a partial de-synchronization of event flows and a sudden reduction of harmonic events density.
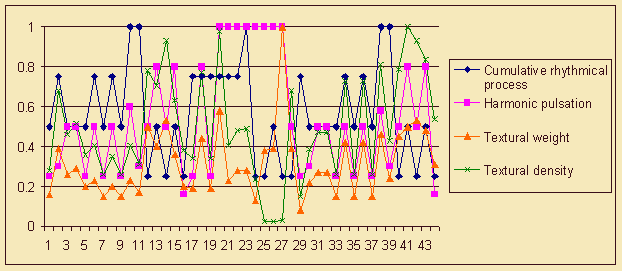
Figure 8. W.A. Mozart. Menuet. Membership functions fR(i) (Cumulative rhythmical process), fH(i) (Harmonic pulsation) and two versions of membership function fT(i) (Textural weight and Textural density).
The presented description allows us to say that within the first part of "Menuet" the distinguished fragments perform the functions of the Russian musicologist Asafyev's "triad" members - initium (1-5 bars), motus (5-11 bars), terminus (12-16 bars), moreover, the fragmentation (division) of "eventive exposition" differs from that of "thematic exposition". If we regard the piece as a whole, we should note the coincidence of the planes of purely musical and eventive structures. At the same time the expositional stage of "events composition" is characterized by parallel changes of density of different types of events, the developing stage - by gradual transition from parallelism of rhythmical and textural flows to independent progress of all flows, and the closing stage - by return to the initial correlation of eventive flows, brought to a higher degree of similarity.
The interpretation of graphs' content built on the basis of events density measurements in the sonata form present a special interest. Let us demonstrate the capabilities of such interpretation on the example of the first part of fortepiano sonata No. 19 by L. Beethoven.
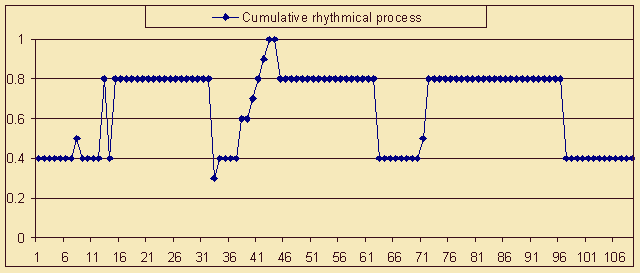
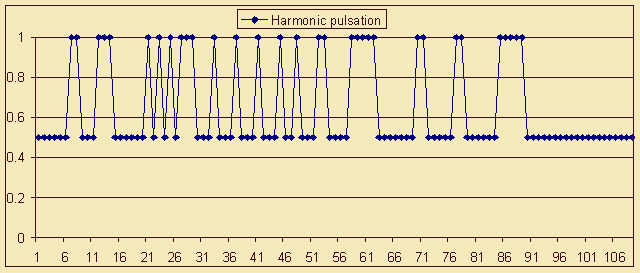
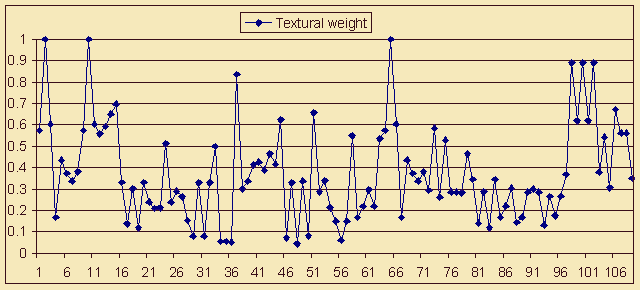
Figure 9. L. Beethoven. Sonata op. 40 No. 1 (part I). Membership functions fR(i) (Cumulative rhythmical process), fH(i) (Harmonic pulsation) and fT(i) (Textural weight).
On the graph in Figure 9 the end of the principal theme is marked by the growth of rhythmical and harmonic events density. This growth underlines openness, incompleteness, typical of classical sonata form, owing to which not only the theme itself, but also the exposition on the whole "demand more insistently than in other forms further musical events and search for new result" (Sokolov, 1974, p. 172). Structural divisions and sub-divisions, which follow the principal theme (up to reprise) are resolved as zones of more or less intensive development. The execution of this compositional function is provided for not only by purely musical, but also by non-specific means, including the growth of events density. Whereas for the principal section of the primary part, the average value of bar saturation with musical events of all types is equal to 1,52, for the connecting part (from 9th to 15th bar) it amounts to 1,61, for the subsidiary part (from 16th to 33rd bar) - to 1, 69, for the development (from 34th to 63rd bar) - to 1,72. From this angle the exceptions are the events of the textural flow - in the developing sections their number is reduced in order to prevent the massiveness of the textural figure interfering with the dynamism of dramaturgic process (and vice versa - in the coda the number of textural events increases, which is clearly outlined at the background of "degenerated" curves of rhythmical and harmonic flows and is conditioned by the necessity to perform the slowdown, the dampening of energy accumulated in the course of preceding development).
In the regarded sections the interaction of compositional division devices dramaturgic incorporation are of special interest. Thus, the border between the principal and the subsidiary parts is emphasized in the 16th bar by the decline of harmonic events density, but is "crossed out" by the rise of rhythmical events density. At the same time the border between exposition and development in the 33rd bar, clearly outlined by the means of rhythmical pattern, is masked by the acceleration of harmonic pulsation. Only one caesura - between development and reprise (in the 63rd bar) turns out the result of unidirectional changes of events density in rhythmical and harmonic flows.
The reprise of "eventive composition" (where the purported result is achieved) features considerable changes of expositional material, mostly felt at the level harmonic pulsation. In the connecting section of the primary part (72-79th bars) the profile of the harmonic curve almost repeats the profile of the principal section, which is logically related to the absence of necessity to "service" the dynamic coupling of the principal and the subsidiary themes. Further on, in the subsidiary part the harmonic relief acquires a generalized outline, directly summing up the peculiarities of preceding structural units: in 85-89th bars a zone of high events density, which brings together not only the harmonic maximums of the primary part, but also the multiple "peaks" of the relevant exposition section. The named peculiarities serve a graphical depiction of themes convergence ("achieving identity"), which is a characteristic feature of sonata reprise. Thus, the built graphs of events density for the first part of fortepiano sonata by L. Beethoven No. 19 can be regarded as an example of a "graphical equivalent" to the sonata principle, which is formulated at the logical level as "comparison, interaction and result" (Sokolov, 1974, p. 173).
Generalizing the results of the performed analysis, we should note that while examining the eventive structure of the piece we deal with two factors determining the participation of musical events density in the formation process:
- with exact values of membership functions, evaluated in terms of this segment of events flow belonging to a certain section of composition, and
- with certain trends of those values changes, i.e. with a certain mode of events dynamics.
In the first case we look at the musical piece in the static aspect - as at a "crystal", possessing architectonical integrity of a solid sound construction, easily memorized. In the second case we mean the dynamic aspect of arranging the artistic content of a musical piece. However, in both cases we have to deal with a "phenomenon of musical simultaneity" described by Rudolf Arnheim: "Evidently in order to create or to understand the structure of a film or a symphony, one has to grasp it as a whole, exactly as one would the composition of painting. It must be apprehended as a sequence, but this sequence cannot be temporal in the sense that one phase disappears as the next occupies our consciousness. The whole work must be simultaneously present in the mind if we are to understand its development, its coherence, the interrelations among its parts" (Arnheim, 1974, p.374). Further on, to illustrate such a phenomenon Rudolf Arnheim cites a letter attributed to W. Mozart: "[when a theme has caught the composer's attention,] it becomes larger and larger, and I spread it out more and more widely and clearly, and the thing really gets to be almost completed in my head, even if it is long, so that thereafter I survey it in my mind at one glance, like a beautiful picture or handsome person. And I hear it in my imagination not in sequence, as it will have to unfold afterward, but, at it were, right away all together (wie gleich alles zusammen)" (Ibid.).
Let us draw some conclusions. The performed examination allows us to say that the dynamics of events density changes belongs to the means, which provide for the realization of universal principles of structural thinking. In order to describe the mechanism of this realization, we will use the classification of musical universals, proposed by Russian musicologist Vyatcheslav Medushevsky (Medushevsky, 1979, pp. 180, 196), adding another level to it, or to be more precise, having separated basic laws typical to various world phenomena, which are non-specific to music, from music-specified ones.
This level comprises the categories of formal logic, rhetoric, dramaturgy and the like, which allow talking about theme identification (according to the formula S is / is not P), realization of rhetoric functions (Exordium, Expositio, etc.), attribution of the examined fragment to a certain stage of dramaturgy (exposition, entanglement, development, etc.).
The second level is formed by music-specified phenomena, laws, categories, including the object of the present study - the musical event. At this level each of the events, possessing a specific sound quality, also acts as a component of exposing, developing or completing musical thought.
And, finally, the third level unites techniques and devices of material organization, specific to music. At this level a concrete event shall be regarded as an element of one of musical grammar systems, immanently subordinated to "rules of musical grammar".
The events of the central layer belong to music in terms of their "material shell", and to non-musical systems (logic, rhetoric, etc.) in terms of their organization. Carrying the organization principle typical of these systems, they are capable of organizing musical motion in the historic periods, when musical logic did not exist in the sphere of their operation. The examples here are the maximum textural density in the closing parts of masses, acceleration of harmonic pulsation rhythm as a means of development in terms of modality, synchronicity or asynchronicity of events minimums as an indicator of caesura depth in polyphonic texture, etc. Such devices are directly linked to non-musical phenomena, among which are the maximum number of singers in a mass final as a result of uniting all the people present in the end of the worship; convergence of syntactic division of musical polyphony as a result of individual speed of reading-intonating the text by the parish; transition to smaller lengths as a result of real increase of musical motion speed, etc. In general, it should be noted that event saturation of musical time units is directly related to reflection of real, logical and rhetoric, artistic and dramaturgic and other processes in sound form.
Based on the above, we can suppose that the realization of artistic capabilities of events dynamics contributed to accumulation of formation potential of specific means and devices. Having ensured the establishment of a purely musical system of formation, non-specified phenomena continued to exist alongside the specific ones, acting as accompaniment or counterpoint, but always staying in their shadow. Those relations change fundamentally, when the technological paradigm of music is revised: over the period of search and "approbation" of new approaches the main load on organizing the formation process falls on non-specific means, among which is the density of musical events, which has become the subject of this study.
Thus, the musicology-oriented analysis of diagrams, built on the basis of mathematic calculations, has fully proved the initial hypothesis about the formation role of events density. Moreover, the subsequent clarification of spiritual implications, which animates sound constructions, allowed us to identify some universal artistic and aesthetic determinants of musical forms.
In those cases, when events dynamics is interpreted chiefly as a means of musical speech division, the primary positions are occupied by such aesthetic and axiological attributes, as adequacy, proportionality, symmetry. Thus, the idea about the form as an architectonics, reflecting certain static integrity, is realized.
Another approach, which models a certain events pattern of development, preparation of culmination and retreat from it, is related to realization of the concept of musical time as a "lifecycle" of a musical organism. The basis of this - dynamic - concept of the form is the reconstruction of motion rhythms of being and thought.
The stated conclusions refer to the field of studying musical expressions of the aesthetic notion of "beauty" as a musical "truth". This circumstance attests the rationality of applying exact (precision) methods in art studies, whereas the results of such researches open the ways to deeper and diversified cognition of artistic phenomena.
REFERENCES
Arnheim R. (1974). Art and visual perception: A psychology of the creative eye. The new version. Berkeley - Los Angeles: Univ. of California press.
Florensky P.A. (1971). Pifagorovy tchisla. Trudy po znakovym sistemam. Tartu. [Pythagorean numbers] (in Russian).
Hindemith P. (1940). Unterweisung im Tonsatz. Mainz.
Kon Yu.G. (1971). Ob odnom svoystve vertikali v atonal'noy muzyke. Muzyka I sovremennost. Edition 7. Moscow: Muzyka [On a vertical property in atonal music] (in Russian).
Kon Yu.G. (1971a). Zametki o ritme v "Velikoy svyashchennoy plyaske" iz "Vesny svyashchennoy" Stravinskogo. In: L.G. Rappoport (Compiler). Teoreticheskiye problemy musykal'nyh form I zhanrov. Moscow: Muzyka. [Notes on rhythm in the "Sacred Dance" from the "Sacre du Printemps" by Stravinsky] (in Russian).
Kulichkin P., Zubareva N. (2004). "Degenerated" cases of tensity function and the degree of genre characteristics expression in a musical piece (experiments of quantitative analysis applied to pianoforte miniatures of XVIII-XX centuries). In: J.P. Frois, P. Andrade & J.F. Marques (Eds.). Art and Science - Proceedings of the XVIII Congress of the International Association of Empirical Aesthetics. Lisbon: Calouste Gulbenkian Foundation, 536-539.
Medushevsky V.V. (1979). O musykal'nyh universaliyah. In: S.S. Skrebkov. Statii I vospominaniya. Moscow: Sovetsky Compositor.[On musical universals] (in Russian).
Ruchyevskaya Ye.A. (1998). Klassitcheskaya musykal'naya forma. Saint-Petersburg: Composer [Classical musical form] (in Russian).
Sokolov O.V. (1974). O printsypah strukturnogo myshleniya v muzyke. In: Aranovsky M.G. (Ed.) Problemy musykal'nogo myshleniya. Moscow, 153-176. [On Principles of Structural Thought in Music] (in Russian).
Zadeh L.A. (1965). Fuzzy sets. Information and Control. Vol. 8, 338-353.